Labour market
The supply side can be described as a price and wage setting model à
To give the reader an intuition about the model properties I show the simplest possible specification (which is different from the BASMOD specification) of such a model. The reader is then referred to the specific parts of the labour market in BASMOD which basically works in the same way.
A Simple Basic Specification
Let the producer wage be . Let the wage equation be represented by the wage share equation
i.e. the wage share depends on the unemployment rate. is an index that measures structural factors in the labour markets, such as the replacement ratio, unemployment insurance, etc. and defined such that it is supposed to have a negative effect on the labour share. Consider then the simple producer price equation
where is the markup (on marginal costs).
It is assumed that the bargaining system is such that it results in real wages that are high enough to let labour demand determine the total number of hours worked. The demand equation is
while the mean number of hours worked is determined by
the real consumer wage rate, where the relation to the producer wage rate is given by
where SETAXR is the direct tax rate and SEITR is the indirect tax rate from which follows the tax wedge
which at the moment is approximately 70 percent. These equations determine employment while the labour force is determined by the equation
and the rate of unemployment residually by the identity
Production functions, cost functions, potential output and marginal cost
From the equilibrium of the labour and capital markets we can calculate potential output and marginal cost. The price mechanism in which prices rise as the economy overheats and fall in a downturn generally depends only on marginal cost and not on the output gap unless in the special case of a Cobb-Douglas technology. However, the Cobb-Douglas technology implies constant factor shares and hence is in conflict with the labour market model above. Discarding the Cobb-Douglas technology also implies that the output gap does not enter the price equation (cannot be substituted for marginal cost). Therefore in deriving demand for labour and marginal cost I have used alternative technologies.
Fairly standard is the CES production function:
where is the capital share of output, is a scale parameter and a parameter that determines the functional form. The elasticity of substitution is . determines the rate at which labour-augmenting technical progress proceed. From this production function we can derive potential output and an output gap by using the steady state values of capital and labour.
The parameters of the above production function can be estimated/calibrated from the labour demand function – which then must include a time trend to capture the labour-augmenting technical progress. In the CES function the parameter determines the functional form and is calibrated to -1.64 and is calibrated to 1.52. The rate of technical progress and the elasticity of substitution are estimated from the labour demand equation.
There is also a cost function corresponding to the production function, which in this case is
where SETC is total cost. The marginal cost can be derived as
which gives the equilibrating mechanism since – as shown below – the price level is determined by marginal cost. Also the input demand equations, for instance for labour demand can be derived as
Two points are worth mentioning. Since the input demand functions and the marginal cost functions are derived from the same cost function they will share the same parameters and those parameters should be identified in the econometric estimation by using cross-equation restrictions in the simultaneous estimation of price and input demand equations. That procedure allows the parameters of both the production and the cost function to be identified.
The above example uses the CES production function and derives potential output and the output gap and the latter can be included in the producer price equation. A drawback is the very simple form of technical progress that is assumed. A case where a flexible functional form is used (the generalised Translog form) and where the technical progress is endogenised and due to the education levels of the employed is used as an alternative. This is derived and estimated in the AMOD model and is presented in Appendix 3. It has also been implemented in BASMOD but is presently not the default. See the BASMOD Web Site for news and more details.
Hence, potential output will be determined by the same factors as the equilibrium rate of unemployment and in addition the labour force and the labour productivity. Potential output will grow in line with labour productivity and the labour force and be affected positively by the degree of competitiveness in the markets. This can be illustrated with a simpler version of the model[1].
In deriving marginal cost, demand for inputs and possibly potential GDP and the output gap it seems crucial to apply a suitable functional form. The Cobb-Douglas form is a very restrictive form in which it is assumed that the elasticity of substitution whereas in the CES it is assumed to be constant. The Cobb-Douglas form implies that the cost shares are constant, a prediction which is very clearly rejected by the Swedish data[2], both in the short and in the long run.
With less restrictive functional forms the elasticity of substitution is allowed to vary. In addition to the CES form above two alternatives is the generalised Leontief function or the Translog model. The (generalised non-homothetic) Translog cost function is
and this cost function is used to generate marginal costs and demand for labour in shares form. A is a labour-augmenting technological factor which is either a time trend as above or depends on certain factors, such as educational levels in the AMOD model. Both types of technological factors have been estimated. The educational model estimates and as the effects of high school ( ) and university education ( ) on productivity in
in a simultaneous equation Translog model where marginal cost (producer price setting) and the demand for labour and capital is estimated simultaneously with theoretical constraints imposed on the parameters in the cost function above[3]. Using this model I estimated the following time series for A:
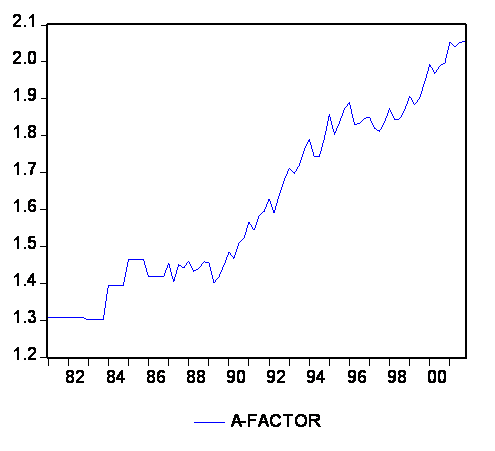
Diagram 1. Estimated for 1981-2002.
It shows that the labour-augmenting technological progress on average is 2.2 percent per year for the period 1981-2002.
A positive technology shock would typically increase the A-factor and effective labour hours, lower the shadow wage rate, increase labour demand, the actual real wage rate and output.